交通运输研究 >

2025 , Vol. 11 >Issue 2: 93 - 104

DOI: https://doi.org/10.16503/j.cnki.2095-9931.2025.02.008

理论与方法

基于GRU-KAN模型的地铁站周边共享单车需求预测

  • 马飞虎 , 1, * ,
  • 肖婷 1 ,
  • 王雪杰 1 ,
  • 孙翠羽 1 ,
  • 李明 2
展开
  • 1 华东交通大学 交通运输工程学院，江西 南昌 330013
  • 2 江西省交通科学研究院有限公司，江西 南昌 330200

马飞虎(1973—)，男，甘肃金昌人，博士，教授，研究方向为交通地理信息、智能交通及3S技术集成与应用。E-mail:

收稿日期: 2024-11-27

  网络出版日期: 2025-06-02

基金资助

江西省03专项及5G项目(20212ABC03W04)

收起

Demand Forecasting of Shared Bicycles Around Subway Stations Based on GRU-KAN Modeling

  • MA Feihu , 1 ,
  • XIAO Ting 1 ,
  • WANG Xuejie 1 ,
  • SUN Cuiyu 1 ,
  • LI Ming 2
Expand
  • 1 School of Transportation Engineering, East China Jiaotong University, Nanchang 330013, China
  • 2 Jiangxi Transportation Research Institute Co., Ltd., Nanchang 330200, China

Received date: 2024-11-27

  Online published: 2025-06-02

Fold

摘要

为准确预测不同地铁站点的共享单车需求量，克服传统模型长时序依赖问题和特征权重分配上的不足，提出基于柯尔莫哥洛夫-阿诺德网络(KAN)改进门控循环单元(GRU)的GRU-KAN预测模型，利用GRU模块提取时间序列特征，KAN模块实现自适应特征加权与非线性关系学习。以深圳市地铁站点为研究对象，首先，对共享单车需求量影响因素的时空特征、气象特征进行可视化，并运用斯皮尔曼相关性分析法分析影响因素的相关性。随后，将共享单车订单数据、气象特征及出行特征输入GRU-KAN模型中，构建需求预测模型。为验证模型的有效性，选取4个代表性站点进行实验，同时与LSTM、BiLSTM、GRU、KAN、LSTM-KAN等模型进行对比分析。实验结果显示，GRU-KAN模型预测精度优于单一的时间序列预测模型及其他组合模型，MAE和RMSE分别平均下降了19.71%、15.20%，R²平均提高了12.38%。进一步，选取不同时段深圳市所有地铁站点的共享单车需求量进行验证。结果显示，GRU-KAN模型在大多数地铁站点预测误差较小，验证了该模型的预测性能，可为共享单车需求预测提供一种新方法。

关键词： 智能交通; 需求量预测; GRU-KAN模型; 神经网络; 时空特征

本文引用格式

马飞虎 , 肖婷 , 王雪杰 , 孙翠羽 , 李明 . 基于GRU-KAN模型的地铁站周边共享单车需求预测[J]. 交通运输研究, 2025 , 11(2) : 93 -104 . DOI: 10.16503/j.cnki.2095-9931.2025.02.008

Abstract

In order to accurately predict the demand for shared bicycles at different subway stations and overcome the problems of long-term sequential dependence and the deficiencies in the assignment of feature weights in traditional models, a GRU-KAN prediction model based on the improvement of the Gated Recurrent Unit (GRU) with the Kolmogorov-Arnold Network (KAN) was proposed. The GRU module was utilized to extract the features of time series, and the KAN module realized adaptive feature weighting and learning of nonlinear relationships. Taking the subway stations in Shenzhen as the research objects, first of all, the spatiotemporal features and meteorological features of the factors influencing the demand for shared bicycles were visualized, and the Spearman correlation analysis method was used to analyze the correlations of influencing factors. Subsequently, the order data of shared bicycles, meteorological features, and travel features were input into the GRU-KAN model to construct a demand prediction model. To verify the effectiveness of the model, four representative stations were selected for experiments, and compared and analyzed with models such as LSTM, BiLSTM, GRU, KAN, LSTM-KAN. The experimental results show that the prediction accuracy of GRU-KAN model is better than that of single time series prediction models and other combined models, with MAE and RMSE decreasing by an average of 19.71% and 15.20% respectively, and R2 increasing by 12.38%. Furthermore, the demands of all subway stations in Shenzhen at different time periods were selected for verification. The results show that the GRU-KAN model has small prediction errors at most subway stations, which verifies the prediction performance of the GRU-KAN model, provides a new method for the prediction of shared bicycle demand.

Key words： intelligent transportation; demand forecasting; GRU-KAN model; neural network; spatio-temporal characterization

0 引言

近年来，共享单车作为一种新兴的城市交通方式，在国内外多个城市迅速普及[1]。众多运营商在城市投入大量共享单车资源，在方便居民出行以及促进环境保护的同时也带来了一系列问题[2-3]，如高峰时期某些地区车辆供应不足，非高峰时期某些地区车辆闲置堆积[4]，占用人行道、地铁站出入口等公共基础设施空间[5]，影响了居民出行体验以及城市形象。因此，如何准确预测共享单车的需求量，优化车辆调度，成为提升其运营效率和用户满意度的关键。
对于共享单车需求预测，目前常用的方法是基于历史订单数据，构建机器学习、深度学习模型预测未来一段时间内的单车需求量。机器学习模型[6-8]在处理多特征数据时表现出色，但较少关注数据的时间序列特征。深度学习模型因其强大的时序数据处理能力，被广泛应用于共享单车需求预测。如Shi等[9]和沈峰等[10]分别利用长短期记忆网络、门控循环单元预测共享单车需求量，研究结果表明，与主流的机器学习模型相比，深度学习模型精度更高。上述研究在提升预测精度方面取得了一定的成果，但是共享单车需求量属于多特征数据，单一的预测模型难以捕捉数据的复杂特征。为此，有研究人员引入注意力机制进行共享单车需求预测，通过增强模型对重要特征的关注度，提升其预测精度，如Peng等[11]将注意力机制与卷积递归神经网络结合，许淼等[12]在长短期记忆网络中融入注意力机制。还有研究人员通过组合不同的模型，如Ai等[13]组合卷积神经网络与长短期记忆网络(Conv-LSTM)预测共享单车需求量，同步解决了共享单车空间依赖性和时间依赖性问题。Zhou等[14]提出基于时间卷积网络(Temporal Convolutional Network, TCN)改进GRU的TCN-GRU预测模型，发挥各模型在提取不同特征上的优势。近期，Kolmogorov-Arnold 网络(KAN)被应用于预测领域。如 Qiu 等[15]将 GRU-KAN 模型用于油井产量预测，结果表明，该模型相比传统单一模型和组合模型，在预测精度和计算效率上均具有显著优势，展现了 KAN 模型在复杂预测任务中的潜力。
上述研究在共享单车需求预测方面取得了一定成果，但也存在一些局限性。首先，现有模型大多仅关注时间依赖性，且存在对输入特征赋予相同权重，难以自适应调整关键影响因素贡献度的问题。其次，现有研究大多聚焦于对整个区域(例如全市范围)的共享单车需求进行预测，此类宏观层面的预测结果对于单车调度缺乏直接的指导意义。鉴于此，本文以深圳市236个地铁站点为研究对象，提出GRU-KAN预测模型，其融合了门控循环单元(GRU)在时序数据分析上的优势与关键注意力网络(KAN)在特征提取上的能力，能有效处理各特征数据之间的复杂关系，提高共享单车需求预测精度，为车辆调度提供支持。

1 数据预处理与共享单车使用特征分析

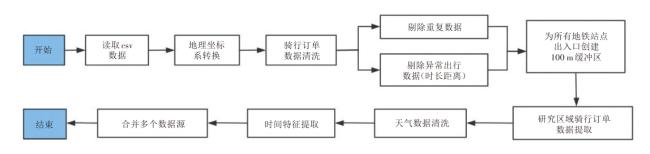
1.1 数据描述与处理

研究区域覆盖深圳市全域，覆盖深圳市内的所有地铁线路及其站点，共包含236个地铁站点。研究数据集涵盖2021年7月1日—7月31日深圳市全天的共享单车使用记录，以及同期深圳市的逐小时气象信息数据。共享单车相关数据来源于深圳市政府开放数据平台，地铁站点信息来源于高德地图，气象信息数据来源于一个提供全球日期、时间、天气等信息的专业网站Time and Date(网址为www.timeanddate.com)。
为预测地铁站点周边区域的共享单车需求量，需精确识别出地铁站点区域内的共享单车骑行订单数据。
首先，为确保数据质量，需对骑行订单数据以及天气数据进行进一步处理。对于骑行订单数据，通过Python进行预处理，剔除重复值、订单信息缺失数据、异常值、骑行时间小于1 min和大于24 h、骑行距离大于20 km的数据后，筛选出特定日期和时段的数据。然后，利用ArcGIS软件，在每个地铁站点的出入口设立100 m的缓冲区，在缓冲区内，无论是共享单车的停车还是使用，都被视为有效的地铁接驳行为[16]。经筛选得到的缓冲区内的共享单车订单数据即为地铁站区域内的共享单车订单数据，最终获得185万条有效记录。对于天气数据的缺失值，采用线性插值法进行填补。完整的数据处理步骤如图1所示。
图1 地铁站点周边区域共享单车数据集处理步骤

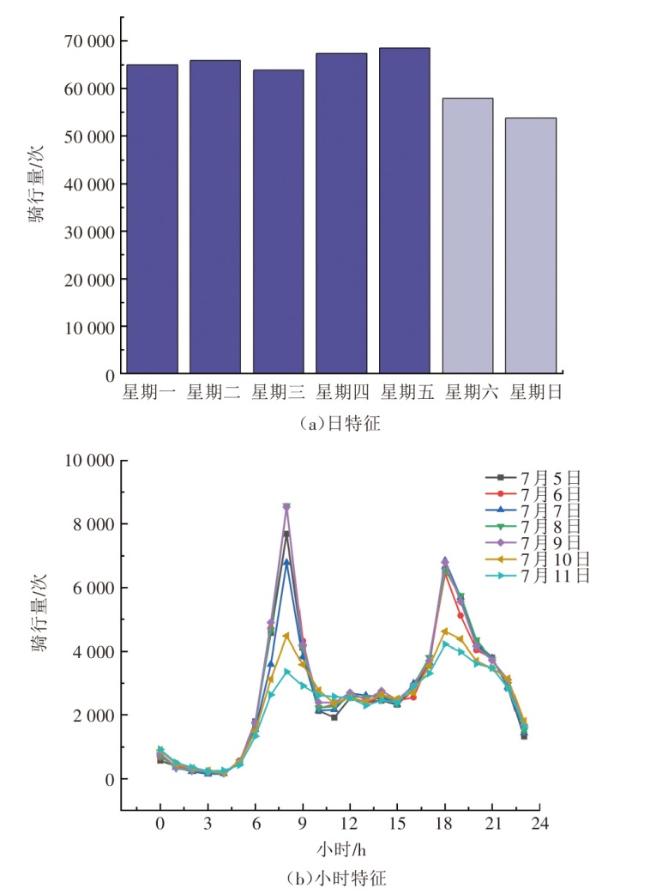
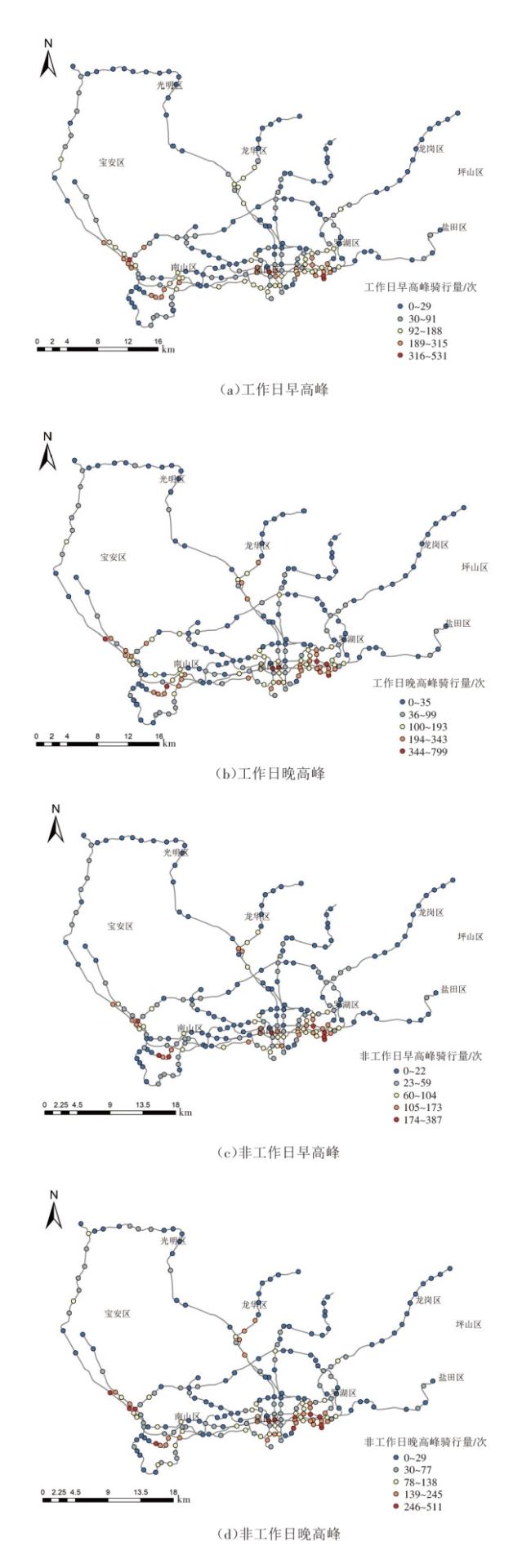
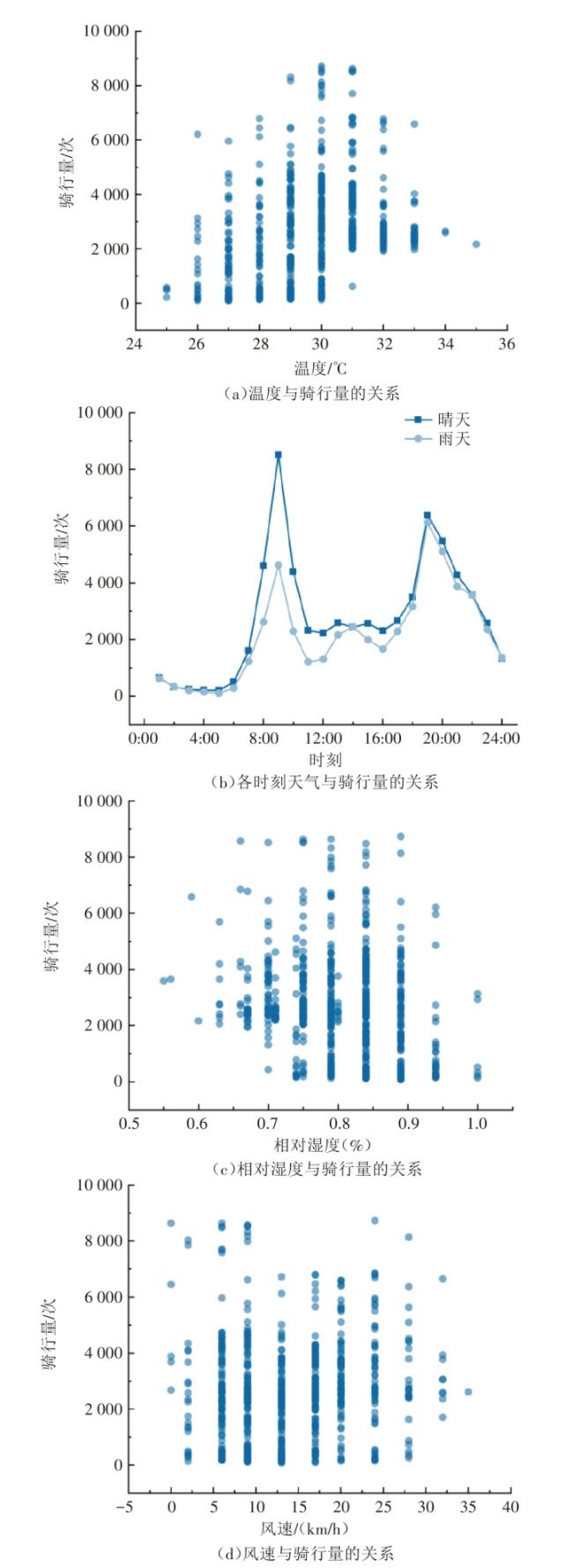
1.2 共享单车使用特征分析

通过对地铁站点区域共享单车使用特征进行分析，可以挖掘出用户的出行模式和规律，识别出热点站点等，有助于预测未来共享单车的使用需求。
1)时间特征
从骑行量日特征(见图2(a))可见，共享单车在工作日与非工作日的骑行需求存在显著区别，其中工作日的骑行量普遍高于非工作日。从骑行量小时特征(见图2(b))来看，骑行量呈现明显的波动性，形成如M形的分布曲线，分别在早晚呈现两个使用高峰。所以，在预测共享单车需求量时，将充分考虑工作日与非工作日的不同需求模式，以及早晚高峰的影响，以提升预测的准确性。
图2 地铁站点区域共享单车骑行量时间特征
2)空间特征
地铁站点区域共享单车骑行量空间特征见图3。由图3可见，共享单车骑行热点区域主要集中在福田区与罗湖区南部交界处、福田区中南部区域、南山区九号线附近、宝安区与南山区交界处、龙华区4号线与6号线交界处。不同地区的共享单车骑行量呈现显著差异。共享单车骑行热点区域的形成与地铁站点周边的功能区分布密切相关。福田区与罗湖区南部交界处紧邻福田CBD和罗湖商业中心，作为深圳市的核心商业区，聚集了大量购物中心和休闲娱乐场所(如深圳万象城、东门夜市等)，吸引了大量出行者，早晚高峰通勤需求旺盛，非高峰时段休闲出行需求也较高。福田区中南部区域是深圳市的行政和文化中心，集中了大量政府机构、写字楼，早晚高峰通勤需求突出，共享单车成为短距离接驳地铁的重要工具。南山区九号线附近是深圳市的科技创新中心，聚集了大量高科技企业，员工通勤需求集中，地铁站点分布密集，共享单车成为短途出行首选。宝安区与南山区交界处是重要交通枢纽，连接宝安机场和南山科技园，周边分布大量住宅区和商业综合体，通勤和商务出行需求较大。龙华区4号线与6号线交界处是新兴居住区和商业中心，以居住功能为主，早晚高峰通勤需求集中，共享单车骑行量较高。
图3 地铁站点区域共享单车骑行量空间特征
3)气象因素特征
除了时空影响外，温度、天气类型等气象因素也影响共享单车的使用需求。共享单车需求量随气象因素变化情况如图4所示。
图4 地铁站点区域共享单车需求量随气象因素变化情况
由图4可知，温度与共享单车需求量存在相关性。深圳市 7 月份温度分布集中在 27 ~32 ℃，该温度范围比较适宜骑行，骑行量较多。天气类型也是影响共享单车出行的重要因素，其对共享单车出行的影响主要表现在晴雨天，晴天的骑行量均高于雨天的骑行量。相对湿度与共享单车骑行量存在一定相关性，在相对湿度较高的天气条件下，共享单车的骑行量可能会受到一定影响。风速对共享单车骑行量的影响相对较小，共享单车需求量在 0~33 km/h风速区间内保持相对稳定。

2 GRU-KAN模型原理及构建

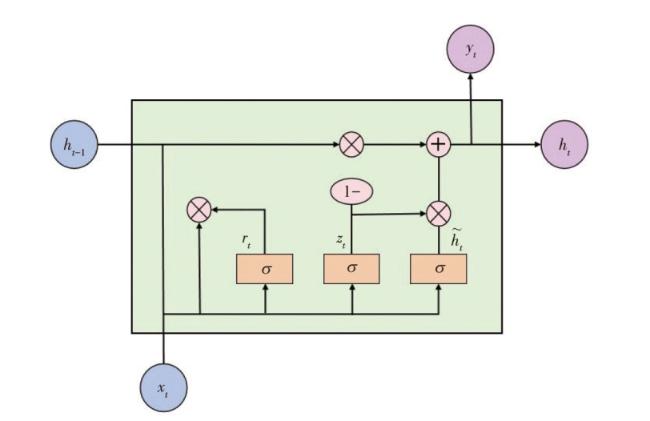
共享单车需求容易受时间(工作日与非工作日、早晚高峰等)、气象(温度、天气类型等)多种因素综合影响，数据呈现复杂的非线性关系和明显的时序特性。传统的时间序列预测模型在处理此类数据时，往往对长时间序列存在过度依赖，难以精准捕捉复杂特征间的关联，导致预测精度欠佳。GRU模型虽在一定程度上简化了循环神经网络结构，提高了训练效率，能处理时间序列数据中的长期依赖关系，但其对所有输入特征赋予相同权重，导致一些不重要的特征可能会干扰预测结果，降低模型预测的精确性。而KAN模型基于Kolmogorov-Arnold理论，采用可学习的激活函数替代传统多层感知机的固定激活函数，能灵活地提取数据的非线性特征，通过为不同部分的输入数据分配不同权重，可突出对预测结果有重要影响的因素。因此，将GRU模型与KAN模型相结合，有望克服各自的局限性，更有效地处理共享单车需求预测中的复杂数据关系，提高预测精度。本文所构建的GRU-KAN组合模型，主要包含GRU模块、KAN模块，模型介绍如下。

2.1 GRU神经网络原理

门控循环单元(Gate Recurrent Unit, GRU)神经网络是循环神经网络(Recurrent Neural Network, RNN)的一种改进版本，其引入两个门控机制——更新门和重置门，以调控信息的传递与遗忘。与长短期记忆网络(Long Short-Term Memory, LSTM)相比，GRU简化了LSTM的结构，使参数量减少，大幅缩短了训练时间，同时依然具备处理长期依赖关系的能力[17]。其两个核心门控机制，即更新门和重置门，能灵活调控信息的流动与存储，使模型能高效地处理时间序列数据，具体网络结构见图5。
图5 GRU神经网络结构示意
GRU通过下列公式[18]实现信息的传递与更新：
z t = σ ( W z [ h t - 1 ,   x t ] + b z )
r t = σ ( W r [ h t - 1 ,   x t ] + b r )
$\tilde{h}_{t}=\tanh \left(W\left[r_{t} h_{t-1}, x_{t}\right]+b\right)$
$h_{t}=\left(1-z_{t}\right) h_{t-1}+z_{t} \tilde{h}$
式(1)~式(4)中： t为当前时刻； x t为 t时刻的共享单车需求量以及特征数据； z t和 r t分别为更新门和重置门； W z, W r, W分别为更新门、重置门和输出层的权重； b z, b r, b分别为更新门、重置门和输出层的系数向量； h t为 t时刻的隐藏状态；$\tilde{h}_{t}$为候选隐藏状态。
在共享单车需求预测中，GRU依据前一时刻的隐藏状态和当前输入特征，通过更新门调整历史信息对当前预测的影响权重，利用重置门调控新输入信息与历史信息的融合，从而高效处理需求数据的时间序列特性。在分析工作日早晚高峰需求变化规律时，GRU可以借助门控机制捕捉到连续时间段内骑行量的增减趋势以及不同工作日之间的相似性。

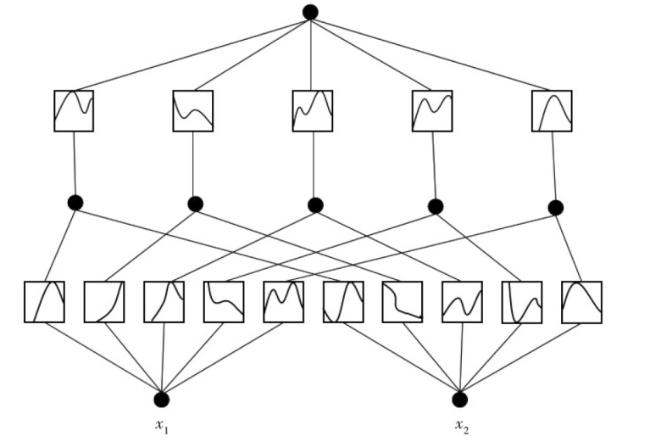
2.2 KAN神经网络原理

柯尔莫哥洛夫-阿诺德网络(Kolmogorov-Arnold Networks, KAN)是一种基于Kolmogorov-Arnold表示定理的新型神经网络框架。其核心思想是：任何复杂的多元函数都可以拆解为多个简单的单变量函数的组合。KAN网络旨在为传统的多层感知机(Multilayer Perceptron, MLP)提供更强的替代。传统的MLP使用固定的激活函数(如ReLU、Sigmoid等)来处理数据，而KAN的创新之处在于采用了可学习的激活函数。具体来说，KAN将网络中的每个权重参数替换为一种被称为样条函数(B-spline)的灵活函数。样条函数是一种通过分段多项式来拟合数据的平滑曲线，能根据数据的变化自动调整形状，更精确地捕捉复杂的非线性关系，使网络在保持灵活性的同时，能以较少的参数实现对复杂网络结构的拟合[19]。KAN网络的整体架构如图6所示。
图6 KAN网络的整体架构
KAN的公式表达基于Kolmogorov-Arnold表示定理展开。以一个简单的形式为例，一个多元函数 f ( x 1 ,   x 2 , ⋅ ⋅ ⋅ ,   x n )可以通过式(5)[20]表示：
f ( x 1 ,   x 2 , ⋅ ⋅ ⋅ ,   x n ) = ∑ q = 1 2 n + 1 Φ q ∑ p = 1 n ϕ q ,   p ( x p )
式(5)中： x 1 ,   x 2 , ⋅ ⋅ ⋅ ,   x n为输入特征； Φ q和 ϕ q ,   p均为单变量连续函数， Φ q为外层函数， ϕ q ,   p为内层函数。在训练过程中，KAN通过 Φ q, ϕ q ,   p构建输入特征与共享单车需求量之间的复杂映射关系。激活函数 ϕ ( x )表达式[20]为：
ϕ ( x ) = w [ b ( x ) + s p l i n e ( x ) ]
b ( x ) = s i l u ( x ) = x / ( 1 + e - x )
s p l i n e ( x ) = ∑ i c i B i ( x )
式(6)~式(8)中： w和 c i均为可学习参数； b ( x )为偏置激活函数，在KAN中该函数被初始化为silu激活函数； s p l i n e ( x )为一组一维函数组合； B i ( x )为预先定义的Base-样条基函数。在训练过程中样条参数 c i持续优化，以调整样条形状，使得能够准确描述特征与需求量之间的非线性关系，从而拟合训练数据。

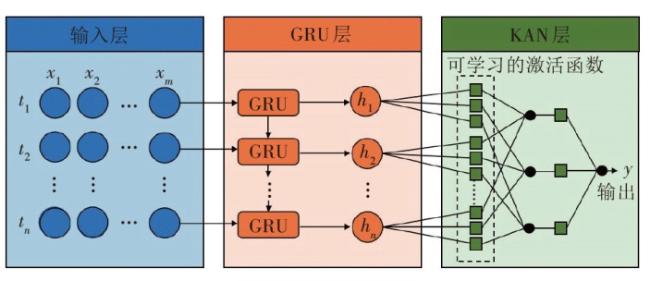
2.3 GRU-KAN共享单车需求预测模型构建

GRU-KAN算法模型的工作流程如图7所示。输入层接受数据预处理后获得的共享单车需求量和特征因素数据，并将其转化为适合GRU神经网络内部可以处理的格式。GRU层用于提取共享单车需求量数据中的时间特征。在每个时间步 t，GRU层接收当前时间步的输入特征(包括历史需求量和特征因素数据)和前一个时间步的隐藏状态，通过门控机制(更新门、重置门)更新隐藏状态，并输出当前时间步的预测结果。将时间序列数据按照时间步依次输入GRU层中，形成序列预测。KAN层通过样条函数将GRU层的输出和原始特征因素数据映射到潜在特征空间。具体而言，KAN层中每个节点使用分段多项式的样条函数拟合输入数据的非线性关系，能根据数据变化自动调整形状，为不同特征分配权重，突出对预测结果有重要影响的因素。最后，通过全连接层将KAN隐藏层的输出转换为共享单车需求量的预测值。
图7 GRU-KAN算法模型的工作流程

2.4 模型评价指标

为了更准确地评估模型对地铁站区域共享单车需求量预测的效果，选取平均绝对误差(Mean Absolute Error, MAE)、均方根误差(Root Mean Square Error, RMSE)和决定系数(R 2)3个评价指标，比较分析GRU-KAN算法模型和对照组算法模型的预测效果，其中相关的计算公式[12]如式(9)~式(11)所示。
E M A E = 1 n ∑ i = 1 n | y i - y ^ i |
E R M S E = 1 n ∑ i = 1 n ( y i - y ^ i ) 2
R 2 = 1 - ∑ i = 1 n ( y ^ i - y i ) 2 ∑ i = 1 n ( y - i - y i ) 2
式(9)~式(11)中： E M A E为平均绝对误差； E R M S E为均方根误差； R 2为决定系数； y i为实际值； y ^ i为预测值； y - i为样本均值； n为预测总数。

3 预测实验分析

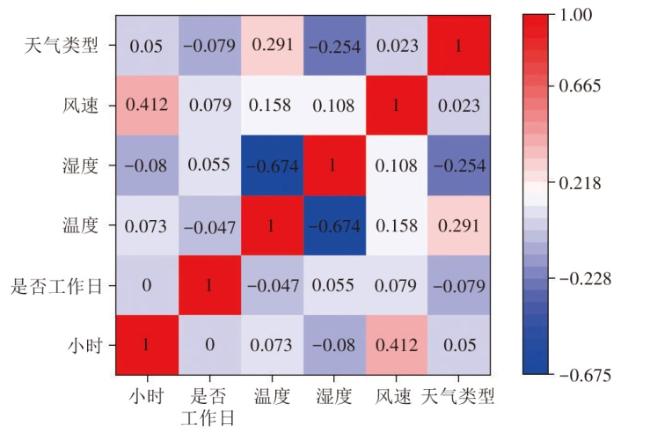
3.1 特征选取与处理

根据共享单车使用特征分析可知，共享单车的需求量受到时间因素和气象因素的共同影响。因此选取是否工作日、小时、温度、天气类型、湿度、风速特征作为自变量，地铁站点的共享单车汇入骑行量作为因变量。各变量概况见表1。
表1 变量概况
变量 指标 变量类型 备注
因变量 共享单车
需求量		 连续型 各地铁站点的共享单车
汇入骑行量/次
自变量 是否工作日 二分类 工作日=1；非工作日=0
时刻 离散型 0: 00—24: 00
(0: 00, 1: 00,…, 23: 00)
温度 连续型 每小时气温/℃
天气类型 二分类 晴天=1；雨天=0
风速/(km/h) 连续型 每小时风速
湿度(%RH) 连续型 相对湿度
为消除不同特征因量纲和数值范围差异对模型训练造成的潜在影响，避免模型过度关注数值范围较大的特征，须对数据进行规范化。这一过程旨在消除量纲带来的偏差，使模型更聚焦于数据的内在变化趋势。数据标准化公式[15]如下：
Z = X - μ σ
式(12)中： Z为标准化值； X为原始数据； μ为数据的平均值； σ为数据的标准差。
对标准化后的特征进行相关性分析，由于各特征之间具有非线性关系，因此，采用适用于非线性关系数据的斯皮尔曼相关系数进行分析。图8为斯皮尔曼相关系数矩阵热力图。由图8可知，各自变量间的斯皮尔曼相关系数均低于0.8，表明自变量之间不存在显著的多重共线性问题，因此无需剔除任何自变量。
图8 相关系数矩阵热力图

3.2 实验设置及参数设置

3.2.1 实验设置

实验采用GRU-KAN模型对地铁站点区域的共享单车需求量进行预测，同时与LSTM、BiLSTM、GRU、KAN、LSTM-KAN等模型进行对比分析，验证GRU-KAN模型对于地铁站点共享单车需求量预测的优势。实验环境为Ubuntu22.04操作系统，处理器型号为AMD Ryzen 9 7900X CPU @3.60GHz, GPU采用NVIDIA GeForce RTX 3090 Ti，基于开源Python环境管理平台Jupyter lab，利用Pytorch中的torch 模块进行模型的搭建及预测。在模型训练过程中，按照8∶2的比例将数据集分割为训练集和测试集。使用训练集对模型进行迭代训练，测试集评估模型的预测准确性。通过调整模型的超参数设置对模型进行多次迭代训练，评估模型预测的精确性。

3.2.2 参数设置

在预测模型的训练过程中，参数设定直接影响模型的优化效果、收敛速度以及最终的预测性能。本次实验训练批尺寸设置为64，此时模型能在泛化能力和训练速度之间取得较好的平衡。学习率对于KAN优化为0.000 5，其他模型均为0.000 3。训练轮数根据实验效果设置为300轮，当训练轮数为300轮时，模型的损失趋于稳定。

3.3 结果分析

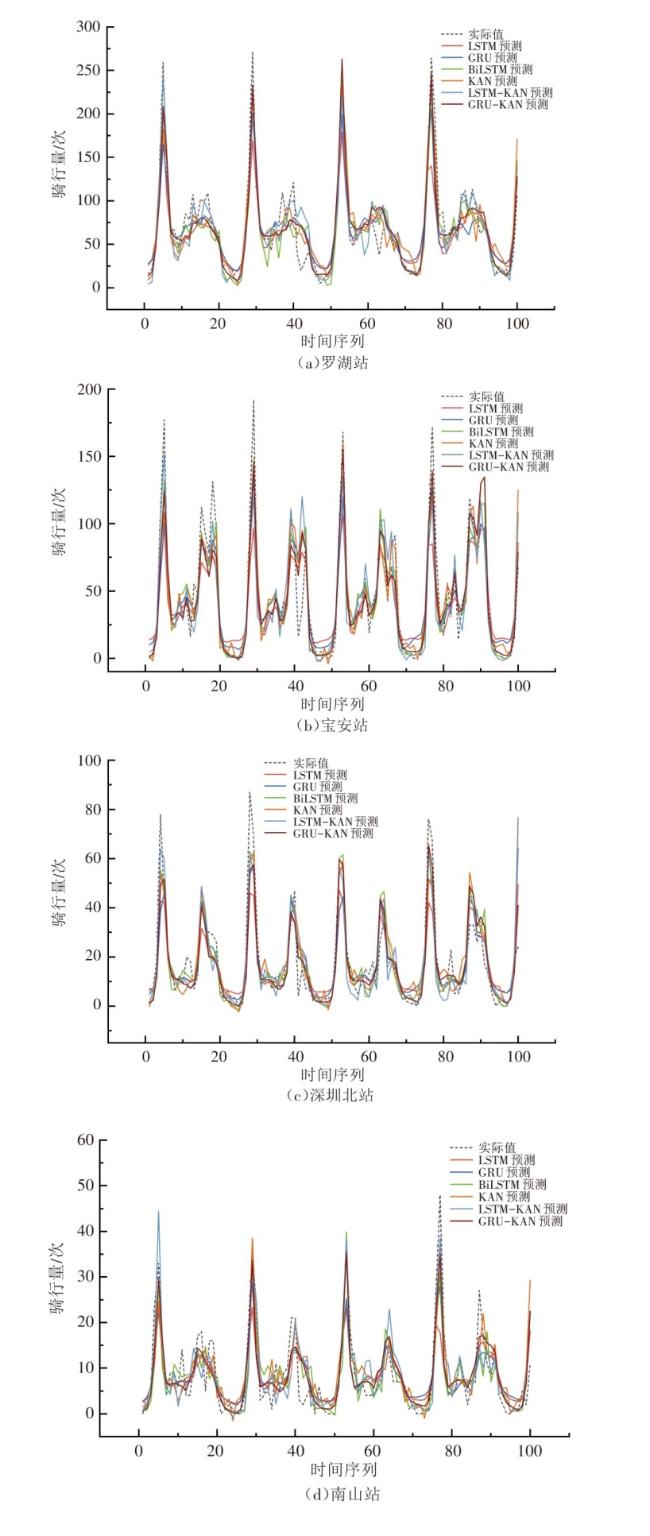
3.3.1 不同站点的预测结果分析

根据共享单车空间特征分析以及各站点共享单车骑行量情况，选取骑行量较高的罗湖站、宝安站和骑行量较低的深圳北站、南山站共4个站点，运用GRU-KAN模型进行需求量预测。为评价模型效果，将GRU-KAN模型预测结果与LSTM、LSTM-KAN、GRU、BiLSTM、KAN模型进行对比，结果如图9所示。
图9 各地铁站点不同预测模型预测值与实际值对比

注：1.图中的骑行量是某一时刻的骑行量。2.横坐标时间序列为共享单车骑行量按发生时间先后顺序排列而成的数列。

从图9可以看出，不管是高流量站点(罗湖站、宝安站)还是低流量站点(深圳北站、南山站)，各模型在高峰时段的预测误差较大，主要原因是高峰时段地铁站周边接驳骑行量受诸多复杂因素交织影响导致需求量激增，传统的LSTM、GRU、BiLSTM模型在捕捉这些波动时表现出一定的局限性，预测误差较大。相比之下，GRU-KAN模型在拟合高峰时段的骑行量方面展现了显著的优势，借助KAN层的特征提取能力，能更好地捕捉高峰时段的需求波动，从而降低预测误差。
为验证不同模型对地铁站点共享单车需求预测的效果，采用MAE、RMSE、R2评价指标进行评价。各预测模型评价指标如表2所示。
表2 各预测模型评价指标
站
点		 评价
指标		 模型
LSTM GRU BiLSTM KAN LSTM-
KAN		 GRU-
KAN
宝
安
站		 MAE/次 16.18 15.82 15.04 11.67 10.15 9.67
RMSE/次 23.44 20.78 20.02 17.26 15.25 14.71
R2 0.68 0.75 0.77 0.83 0.87 0.89
罗
湖
站		 MAE/次 16.99 15.07 16.52 16.80 15.48 13.59
RMSE/次 25.23 21.75 22.54 22.80 22.21 20.23
R2 0.72 0.80 0.78 0.77 0.79 0.83
深
圳
北
站		 MAE/次 6.48 6.18 6.32 5.85 5.69 5.40
RMSE/次 9.46 9.23 8.92 8.81 8.69 8.35
R2 0.69 0.70 0.72 0.73 0.73 0.77
南
山
站		 MAE/次 4.13 4.13 4.01 3.73 3.39 3.18
RMSE/次 5.62 5.61 5.47 4.98 4.81 4.42
R2 0.58 0.58 0.60 0.67 0.69 0.75
由表2可知，LSTM模型在本次预测实验中表现相对较差，主要归因于LSTM模型在处理复杂非线性关系时可能存在一定的局限性。相比之下，GRU模型凭借更简洁的门控结构，在中短序列预测中展现出更高的计算效率和适应性，对4个典型站点骑行量的预测精度均优于LSTM模型。本次实验中，相比于LSTM模型以及GRU模型，BiLSTM模型效果较优，主要原因在于BiLSTM模型在结构上更为复杂，在某些情况下可能具有更强的建模能力。但是其预测效果并未显著优于GRU模型，且BiLSTM模型的复杂结构也增加了其训练难度和计算成本。GRU-KAN模型在RMSE、MAE和R2这3个评价指标上均优于其他对比模型。与LSTM、GRU、BiLSTM、KAN、LSTM-KAN模型相比，GRU-KAN模型的MAE分别平均降低了约27.27%、22.72%、23.99%、16.32%、8.27%；RMSE分别平均降低了约25.16%、16.84%、16.22%、11.40%、6.38%；R2分别平均提高了约21.35%、14.49%、12.89%、8.00%、5.19%，表明GRU-KAN模型在预测共享单车需求量时具有较高的精确性。

3.3.2 不同时段的预测结果分析

GRU-KAN模型在以上代表性地铁站点的预测中表现出良好的性能。为进一步验证其预测效果，采用GRU-KAN模型对深圳市所有地铁站点的共享单车需求量进行预测，选取早高峰、平峰、晚高峰各时段部分结果进行展示，如图10所示。
图10 各地铁站点不同时刻GRU-KAN预测模型预测值与实际值对比

注：横坐标为站点编号。

可以看出，GRU-KAN模型在大多数站点的预测值与实际值吻合度较高，预测误差较小，验证了GRU-KAN模型在地铁站点共享单车需求量预测中的准确性和适用性。

4 结束语

本文考虑了时间、气象等因素对共享单车骑行需求的影响，结合GRU算法的时序数据处理能力和KAN算法提取关键特征的优势，提出GRU-KAN预测模型，有效提升了地铁站点区域共享单车需求预测精度。实验结果显示，在4个代表性站点的预测中，GRU-KAN模型相比于常用的预测模型，在MAE、RMSE、R2这3个评价指标上均表现最优，展现了其在预测精度上的优势。并且在不同时刻深圳市所有地铁站点的预测中，GRU-KAN模型的预测误差控制在较小范围，展现出良好的适用性。通过精准预测地铁站点的共享单车需求量，有助于运营商根据不同站点和时段的需求，合理调配车辆资源，缓解高峰时期的供不应求与非高峰时期的车辆闲置问题，提升运营效率，增强用户使用体验。
本文仍存在一些不足，如：数据样本较少，仅为深圳市一个月的数据，未来研究可扩大数据时间跨度，引入节假日、空间出行特性等更多影响因素，提高模型准确性。随着大数据、人工智能和深度学习的发展，未来研究可以利用更先进的大数据采集和处理技术获取更丰富的数据，探索基于Transformer等新型深度学习架构的改进模型，进一步提升共享单车需求预测的精度和可靠性以及提升模型的可解释性和实时性。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
罗越. 考虑共享单车接驳的公共交通系统设计与优化[D]. 大连: 大连海事大学, 2022.

[2]
王光荣. 共享单车发展问题系统探究[J]. 长安大学学报(社会科学版), 2017, 19(2):30-35.

[3]
ZHANG Y, MI Z. Environmental benefits of bike-sharing: A big data-based analysis[J]. Applied Energy, 2018, 220(15): 295-301.

[4]
常山, 宋瑞, 何世伟, 等. 共享单车故障车辆回收模型[J]. 吉林大学学报(工学版), 2018, 48(6):1677-1684.

[5]
郭鹏, 林祥枝, 黄艺, 等. 共享单车:互联网技术与公共服务中的协同治理[J]. 公共管理学报, 2017, 14(3):1-10.

[6]
NGENI F, KUTELA B, CHENGULA J, et al. Prediction of bike-sharing station demand using explainable artificial intelligence[J]. Machine Learning with Applications, 2024, 17: 100582. DOI:https://doi.org/10.1016/j.mlwa.2024.100582.

[7]
TORRES J, JIMENEZ-MERONO E, SORIGUERA F. Forecasting the usage of bike-sharing systems through machine learning techniques to foster sustainable urban mobility[J]. Sustainability, 2024, 16 (16): 6910. DOI:10.3390/su16166910.

[8]
ALI A, SALAH A, BEKHIT M, et al. Divide-and-train: A new approach to improve the predictive tasks of bike-sharing systems[J]. Mathematical Biosciences and Engineering, 2024, 21(7): 6471-6492.

[9]
SHI Y, ZHANG L, LU S, et al. Short-term demand prediction of shared bikes based on LSTM network[J]. Electronics, 2023, 12 (6): 1381. DOI:10.3390/electronics12061381.

[10]
沈峰, 张璐, 吉静. 基于Res-GRU模型的共享单车骑行量预测和影响因素分析[J]. 交通与运输, 2023, 39(5):70-74.

[11]
PENG Y, LIANG T, HAO X, et al. CNN-GRU-AM for shared bicycles demand forecasting[J]. Computational Intelligence and Neuroscience, 2021, 2021 (1): 5486328. DOI:https://doi.org/10.1155/2021/5486328.

[12]
许淼, 刘宏飞. 基于AM-LSTM模型的共享单车时空需求预测[J]. 湖南大学学报(自然科学版), 2020, 47(12):77-85.

[13]
AI Y, LI Z, GAN M, et al. A deep learning approach on short-term spatiotemporal distribution forecasting of dockless bike-sharing system[J]. Neural Computing and Applications, 2019, 31 (5): 1665-1677.

[14]
ZHOU S, SONG C, WANG T, et al. A short-term hybrid TCN-GRU prediction model of bike-sharing demand based on travel characteristics mining[J]. Entropy, 2022, 24 (9): 1193. DOI:https://doi.org/10.3390/e24091193.

[15]
QIU B, ZHANG J, YANG Y, et al. Research on oil well production prediction based on GRU-KAN model optimized by PSO[J]. Energies, 2024, 17 (21): 5502. DOI:https://doi.org/10.3390/en17215502.

[16]
马君泽, 郑长江, 吴非, 等. 面向地铁站点的共享单车接驳出行特征及影响因素分析[J/OL]. 吉林大学学报(工学版), 2024:1-13. https://doi.org/10.13229/j.cnki.jdxbgxb.20240009.

[17]
张驰, 郭媛, 黎明. 人工神经网络模型发展及应用综述[J]. 计算机工程与应用, 2021, 57(11):57-69.

[18]
钟林岚, 张安勤, 田秀霞. 基于周期图卷积与多头注意力GRU组合的交通流量预测模型[J]. 计算机应用研究, 2024, 41(4):1041-1046.

[19]
SHUKLA K, TOSCANO J, WANG Z, et al. A comprehensive and fair comparison between MLP and KAN representations for differential equations and operator networks[J]. Computer Methods in Applied Mechanics and Engineering, 2024, 431: 117290. DOI:https://doi.org/10.1016/j.cma.2024.117290.

[20]
刘灿锋, 孙浩, 东辉. 结合Transformer与Kolmogorov Arnold网络的分子扩增时序预测[J]. 图学学报, 2024, 45(6):1256-1265.

Options
文章导航

/

〈 〉

版权所有 © 《交通运输研究》编辑部　
京公网安备 11010102003417号    京ICP备17006742号-3
地址：北京市朝阳区北土城东路11号北京书院办公楼　邮编：100029
Email：jtysyj@vip.163.com
本系统由北京玛格泰克科技发展有限公司设计开发