0 引言
1 问题描述
1.1 问题分析
1.2 问题假设
1.3 主要参数
2 选址优化模型
2.1 模型目标
2.2 约束条件
3 算法设计
3.1 模型线性化处理
3.2 Epsilon约束法
4 案例分析
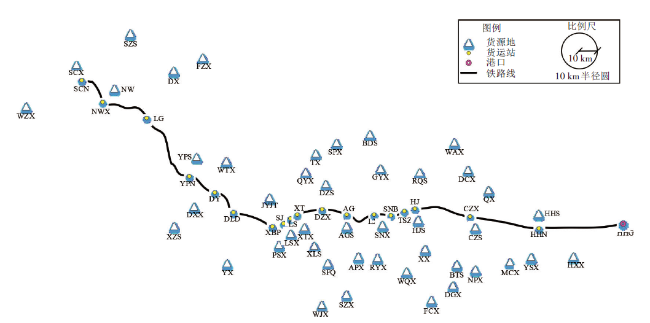
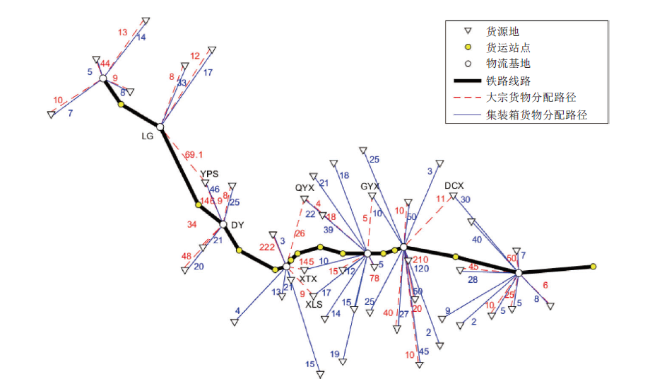
4.1 基础数据
表1 货源地运输需求 单位:万t |
| 货源地 | 大宗货物 | 集装箱货物 | 货源地 | 大宗货物 | 集装箱货物 | 货源地 | 大宗货物 | 集装箱货物 |
|---|---|---|---|---|---|---|---|---|
| JYJT | 222 | 3 | AGS | 15 | 12 | PSX | 0 | 13 |
| YPS | 216 | 46 | SZS | 13 | 14 | LSX | 0 | 21 |
| HJS | 210 | 120 | FZX | 12 | 17 | DZS | 0 | 39 |
| XTX | 145 | 10 | DCX | 11 | 30 | SPX | 0 | 18 |
| SNX | 78 | 5 | WZX | 10 | 7 | SFQ | 0 | 14 |
| HHS | 50 | 7 | RQS | 10 | 50 | WJX | 0 | 15 |
| XZS | 48 | 20 | FCX | 10 | 45 | SZX | 0 | 19 |
| CZS | 45 | 28 | MCX | 10 | 5 | BDS | 0 | 25 |
| SCX | 44 | 5 | NW | 9 | 8 | APX | 0 | 15 |
| WQX | 40 | 27 | XLS | 9 | 17 | RYX | 0 | 25 |
| DXX | 34 | 21 | DX | 8 | 33 | WAX | 0 | 3 |
| QYX | 30 | 22 | WTX | 8 | 25 | QX | 0 | 40 |
| YSX | 25 | 5 | HXX | 6 | 8 | BTS | 0 | 9 |
| XX | 20 | 50 | GYX | 5 | 10 | NPX | 0 | 2 |
| TX | 18 | 21 | YX | 0 | 4 | DGX | 0 | 2 |
表2 货运场站参数取值 |
| 货运 场站 | 既有能力 /万t | 能力上限 /万t | 铁路货运作业设施单位能力 建设成本/(元/t) | |
|---|---|---|---|---|
| 大宗货物 | 集装箱 | |||
| SCN | 200 | 500 | 5 | 11 |
| NWX | 0 | 200 | 20 | 25 |
| LG | 90 | 300 | 10 | 15 |
| YPN | 90 | 150 | 5 | 15 |
| DY | 200 | 380 | 5 | 11 |
| DLD | 90 | 90 | 10 | 15 |
| XBP | 180 | 380 | 5 | 15 |
| SJ | 180 | 480 | 5 | 15 |
| LS | 60 | 150 | 8 | 15 |
| XT | 150 | 580 | 5 | 15 |
| DZX | 70 | 70 | 20 | 25 |
| AG | 120 | 300 | 5 | 15 |
| LX | 140 | 410 | 8 | 11 |
| SNB | 110 | 150 | 8 | 11 |
| TSZ | 60 | 180 | 5 | 11 |
| HJ | 140 | 900 | 5 | 11 |
| CZX | 60 | 370 | 5 | 11 |
| HHN | 80 | 620 | 8 | 11 |
| HHG | 210 | 1800 | 8 | 11 |
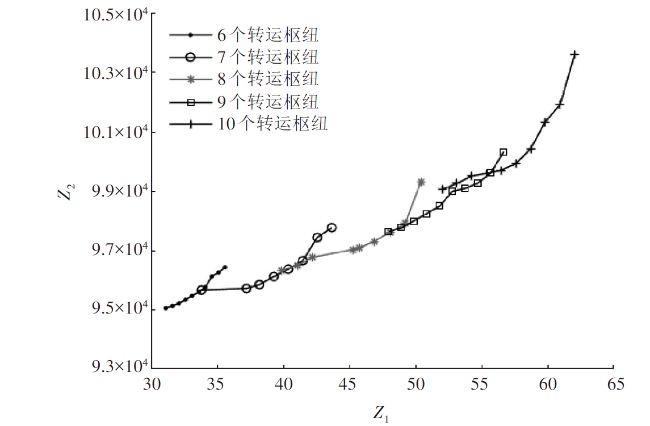
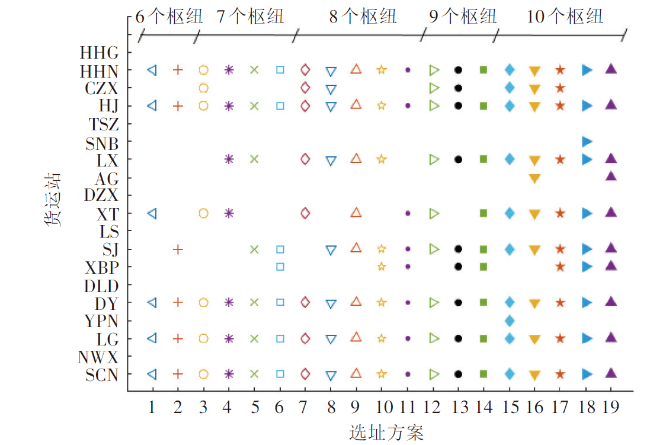
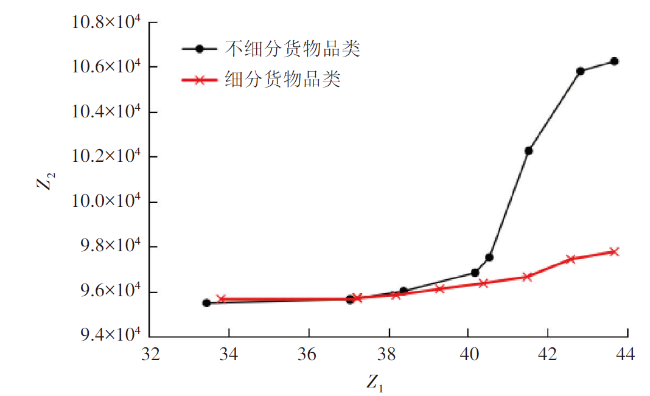
4.2 求解结果
表3 选址方案和目标值 |
| 方案 | 选址位置 | Z1 | Z2 | Z21 | Z22 |
|---|---|---|---|---|---|
| 1 | SCN, LG, DY, XT, HJ, CZX, HHN | 33.81 | 95 667.56 | 40 247.00 | 55 420.56 |
| 2 | SCN, LG, DY, XT, LX, HJ, HHN | 37.22 | 95 721.19 | 40 014.00 | 55 707.19 |
| 3 | 38.20 | 95 850.27 | 39 938.89 | 55 911.38 | |
| 4 | 39.29 | 96 121.19 | 39 942.22 | 56 178.97 | |
| 5 | SCN, LG, DY, SJ, LX, HJ, HHN | 40.39 | 96 371.24 | 39 816.67 | 56 554.57 |
| 6 | 41.48 | 96 657.74 | 39 841.11 | 56 816.63 | |
| 7 | SCN, LG, DY, XBP, SJ, HJ, HHN | 42.58 | 97 439.56 | 39 757.56 | 57 682.01 |
| 8 | 43.68 | 97 773.60 | 39 742.00 | 58 031.60 |